Imagine you’re playing tug-of-war. The rope you’re pulling on feels heavy, doesn’t it? That heaviness is due to a force called “tension.” Tension force is essentially the pull exerted by a string, rope, cable, or similar when it’s attached to an object or objects. It keeps things like bridges suspended and elevators moving up and down. Understanding how to calculate this force is crucial in fields ranging from engineering to physics and even in everyday life. Now, let’s explore different methods to determine the tension force in various scenarios, along with some tips and tricks on the subject.
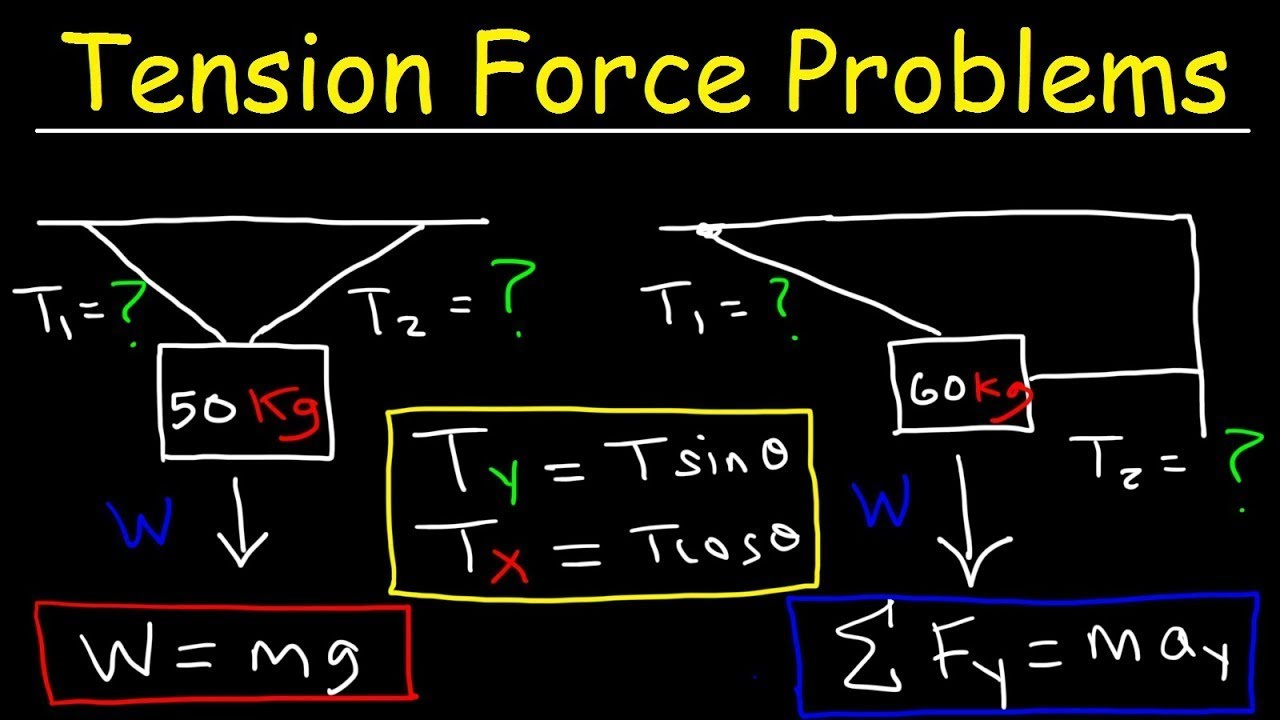
Using Newton’s Second Law
The tension force can often be calculated using the laws of motion established by Sir Isaac Newton. When an object is in motion, Newton’s Second Law can be used to work out the tension in the system.
- Write down the mass (m) of the object being moved or lifted.
- Determine the acceleration (a) of the object. Remember that gravity is an acceleration too, at approximately 9.8 m/s downward.
- Apply Newton’s Second Law, F=ma, to the object to find the force (F) it’s exerting.
- If there’s no other force acting on the object except gravity and tension, the tension in the rope is equal to the force calculated.
Summary:
Calculating tension with Newton’s Second Law allows you to understand the dynamics of an object under force. It’s straightforward but does require an understanding of forces and acceleration. A potential downside is that it assumes no other forces act on the system, which is not always the case.
Through Static Equilibrium
When an object is at rest or moving at a constant velocity, it’s said to be in static equilibrium. In this case, the sum of all forces acting upon it is zero.
- Determine the forces acting on the object. This may include gravity, friction, or other known forces.
- Set the sum of forces in the vertical direction equal to zero, as the object is not accelerating.
- Solve the equation for the unknown tension force, since other forces (like weight, which equals mass times gravity) are typically known.
Summary:
This is ideal for objects that aren’t accelerating. Using static equilibrium is a simple and effective way to calculate tension. However, it may become complex if there are a lot of different forces to consider.
Inclined Plane Tension
Calculating tension on an inclined plane requires considering the weight’s components parallel and perpendicular to the surface.
- Determine the angle of the inclined plane (θ).
- Calculate the force of gravity (weight) parallel to the inclined plane which is w*sin(θ), where w is the weight of the object.
- The tension force is calculated by balancing this force with any applied force and friction.
Summary:
This is suitable for calculating the tension of an object on a slope. It factors in gravity in a more nuanced way but requires an understanding of trigonometric functions.
Centripetal Tension for Circular Motion
When an object is moving in a circle, the tension in the rope provides the centripetal force required to keep it moving in that circle.
- Find the mass (m) of the object.
- Determine the radius ? of the circle along which the object is rotating.
- Measure the velocity (v) of the object.
- Use the formula for centripetal force, ( F_c = frac{mv^2}{r} ), to find the tension.
Summary:
This method is valuable when dealing with rotational systems but can be quite challenging to understand and apply without a good grasp of circular motion physics.
Pulley System Tension
Calculating the tension in a pulley system can become complex, but it’s commonly done by analyzing the forces on each mass and the pulleys separately.
- List all the masses in the system and their respective weights (w).
- If the pulleys are frictionless and the ropes weightless, the tension throughout the rope is constant.
- Use equilibrium equations for each mass and pulley to find the tension.
Summary:
This is suitable for a system of objects connected by a pulley. This method requires careful consideration of the entire system’s balance but can simplify otherwise complex scenarios. The downside is the assumption of an ideal system with no friction.