Understanding the concept of volume is essential in the world of chemistry. It refers to the amount of space an object or substance occupies and is a fundamental measurement for mixing reagents, understanding substance densities, and predicting reactions. Grasping how to calculate volume will empower you to better comprehend and execute chemical experiments with accuracy. Whether you’re a student, educator, or enthusiast, acquiring the skill to determine volume is a stepping stone to mastering chemistry’s practical applications.
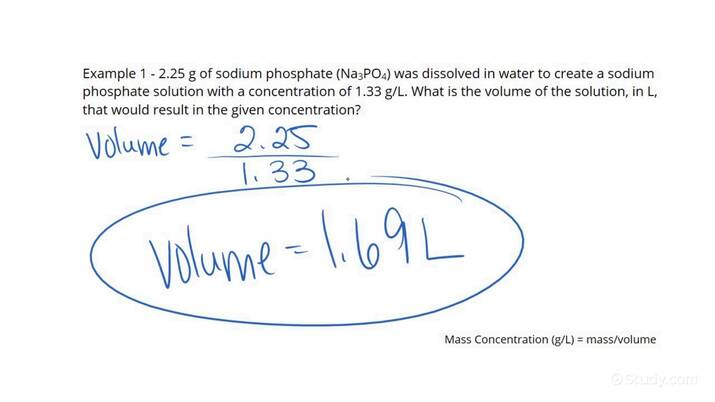
Direct Measurement
When it comes to calculating the volume of a liquid, the most straightforward method involves using measuring tools designed for this purpose, such as graduated cylinders or volumetric flasks.
- Start by choosing the appropriate measuring tool. Graduated cylinders offer a range of volumes and are suitable for most purposes, whereas volumetric flasks are used when a specific, fixed volume is required.
- Place the measuring tool on a stable, level surface and bring your eye to the level of the meniscus, the curved surface of the liquid. Read the volume from the bottom of the meniscus to ensure accuracy.
- Pour the liquid into the measuring tool until it reaches the desired mark. Be precise and adjust as necessary, adding more liquid or removing some with a pipette if you’ve gone over the mark.
Overall, direct measurement is highly effective for liquids and offers straightforward, accessible means for accurate volume determination. However, the accuracy can be influenced by the user’s ability to read the meniscus correctly and the quality of the measuring tool.
Water Displacement
For irregularly shaped objects that cannot have their volume measured directly, the water displacement method serves as a unique solution. Archimedes’ principle states that the volume of the object submerged in water is equal to the volume of the water displaced.
- Fill a graduated cylinder or overflow can with water to a certain level.
- Record the initial volume of the water.
- Slowly submerge the object into the water. Ensure it is fully submerged without touching the sides or bottom if possible.
- Record the new water level once the object is submerged.
- Subtract the initial water volume from the final water volume. The difference between the two is the volume of the object.
The water displacement method is beneficial for its simplicity and the ability to measure objects with complex shapes. However, it’s limited to objects that don’t absorb water and can be fully submerged.
Calculations for Regular Shapes
Calculating the volume of regular geometric shapes relies on mathematical formulas. Each shape, such as a cube, sphere, or cylinder, has its own formula.
- Identify the shape of the object.
- Measure the dimensions of the object. For example, measure the length, width, and height for a rectangular prism.
- Apply the specific formula for the shape. A cube’s volume is calculated as the length of one side cubed (l), while a rectangular prism’s volume is found by multiplying length, width, and height (l × w × h).
- Ensure that all measurements are in the same unit when calculating the volume, typically cubic centimeters or meters for solids in chemistry.
This method is favorable for its precision with regular objects. The downsides are that it only works for specific shapes and it requires accurate measurement of all dimensions.
Gas Volume Relationships
In chemistry, gases react in ways that allow prediction of their volume at different conditions using the Ideal Gas Law. The law is PV = nRT, with P representing pressure, V volume, n moles of gas, R the constant, and T temperature.
- Understand the conditions under which the gas is measured. Note the existing temperature, pressure, and volume.
- If calculating volume based on a change in conditions, use the combined gas law, which relates two sets of conditions: (P1 × V1)/T1 = (P2 × V2)/T2.
- Plug in the known values to solve for the unknown volume.
- When using these gas laws, always ensure that units are consistent. Temperature must be in Kelvin, and pressure must be in atmospheres or another consistent unit.
Though this method is useful for predicting gas reactions, it requires an understanding of gas behavior and careful attention to units and conversion factors.
Dilution Calculations
Dilution involves reducing the concentration of a solution. The formula used is C1V1 = C2V2, where C is concentration and V is volume.
- Determine the initial concentration and volume of the solution, as well as the final desired concentration.
- Use the formula to solve for the final volume needed to achieve the desired dilution.
- Add solvent to the original solution until the calculated final volume is reached.
Dilution calculations are useful in preparing solutions of desired concentration but require precise measurements for accurate results.
Molarity and Volume Relationships
Molarity is a measure of concentration signifying the number of moles of a solute per liter of solution. It’s essential for stoichiometric calculations in reactions.
- To find the volume of a solution, you must know the molarity and the amount of solute. The formula is V = n/M, with n representing moles of solute, and M the molarity.
- If you have the volume and need to find the molarity, use M = n/V.
- Use these formulas to prepare solutions with specific molarity or to scale reactions.
Though the calculations can be straightforward, they require an accurate count of the moles of solute which might be complex to determine.
Percentage Concentration
Percent concentration is another way to express the composition of a solution, useful when preparing laboratory reagents.
- Calculate mass or volume percent by dividing the mass or volume of the solute by the total mass or volume of the solution and multiplying by 100.
- Use these calculations to mix solutions with desired percent concentrations.
This method is widely used but becomes complex with solutions that involve reactions or temperature-dependent volumes.
Molality and Volume
Molality is the number of moles of solute per kilogram of solvent; it’s unaffected by temperature changes.
- Determine moles of solute and mass of solvent to calculate molality.
- If volume is needed, use the density of the solvent to find the mass and then calculate the volume.
This calculation is accurate for temperature-sensitive solutions but requires knowing the solvent’s density.
Using Density
Density is mass per unit volume. To find the volume of a substance given its mass and density, use the formula V = m/ρ, where m is mass and ρ is density.
- Measure the substance’s mass.
- Divide by its density to calculate the volume.
This approach is valuable for calculating volumes of solutions and solids but requires accurate density values.
Stoichiometry
Stoichiometry involves using balanced chemical equations to predict the volume of gas produced or consumed in a reaction.
- Balance the chemical equation.
- Use the ideal gas law or molarity to relate moles of substances to volume.
- Apply stoichiometric ratios to find the volume of the desired gas.
While powerful for predicting volumes in reactions, stoichiometry requires balance and mole-to-volume conversions, which can be challenging for beginners.
To conclude, understanding the various methods for calculating volume in chemistry is crucial for experimentation, research, and industrial applications. Techniques range from simple measurements to complex mathematical calculations and require different levels of understanding and tools. Therefore, learning to choose and correctly apply these methods can significantly benefit anyone working in or studying chemistry, allowing for more accurate and reliable results in chemical practices.
FAQs
- Why is volume measurement important in chemistry?
- How do you measure the volume of an irregularly shaped object?
- What is the difference between molarity and molality in relation to volume calculations?







