How to Calculate Average Percentage a Comprehensive Guide

Understanding the average percentage helps in various aspects of daily life, from analyzing test scores to evaluating business growth. It’s a metric that brings together individual percentages to find their overall effect. This guide is tailored to help you grasp this concept with ease, providing a series of methods and practical advice, ensuring that by the end, calculating an average percentage feels as simple as tying a shoelace.

Traditional Averaging Method

When you think of calculating an average percentage, the most straightforward approach is the traditional averaging method. This technique is best suited for when you have a set of percentages that are equally significant, and you want to determine their collective impact.

Steps:

1. List all percentages: Begin by writing down every percentage you want to include in the calculation.
2. Sum the percentages: Add all the percentages together to get a total sum.
3. Count the numbers: Determine how many percentages you have in your list.
4. Divide the total sum by the count: Take the sum of your percentages and divide it by the number of percentages you counted. This gives you the average.
5. Express the result as a percentage: Make sure your result is expressed in percentage form.

Summary:

The traditional averaging method is intuitive and efficient for straightforward cases. However, if the percentages are weighted differently (some are more significant than others), this method might not provide a true reflection of the average.

Weighted Average Technique

Some percentages carry more weight than others, depending on their significance or impact. The weighted average technique takes this into account, offering a more nuanced understanding of the average percentage.

Steps:

1. List each percentage with its weight: Write down every percentage alongside its corresponding weight (the importance or size it represents).
2. Multiply each percentage by its weight: For each percentage, perform a multiplication by its respective weight.
3. Sum the weighted values: Add all the weighted values together to get a weighted total.
4. Sum the weights: Total up all the weights you’ve listed.
5. Divide the weighted total by the sum of weights: To find the average, divide the weighted total by the total sum of weights.
6. Express the result as a percentage: Ensure your final average is in percentage form.

Summary:

Weighted averages give a more balanced view when percentages are not equally important. However, calculating the weights and their correct application can be tricky, and small errors can largely affect the result.

Using Excel or Spreadsheet Programs

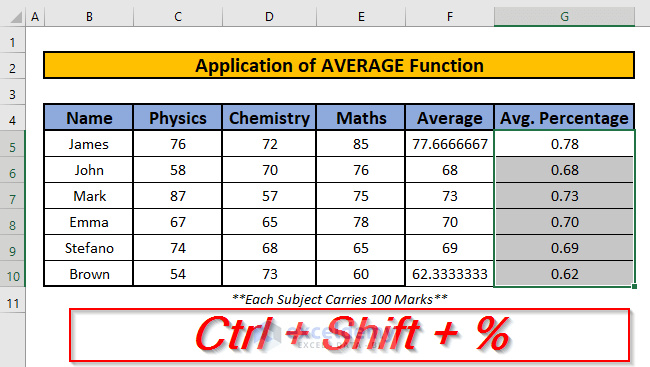
Excel and similar spreadsheet programs offer tools to quickly calculate average percentages, even with large datasets, thus saving time and minimizing manual errors.

Steps:

1. Enter percentages in a column: List your percentages in a single column of a spreadsheet.
2. Use the AVERAGE function: Click on an empty cell and use the AVERAGE function, selecting the range of cells with your percentages.
3. Press Enter: Once you have entered the function, pressing Enter will display the average percentage.
4. Format as percentage: If necessary, format the cell to ensure the result is shown as a percentage.

Summary:

Using a spreadsheet program streamlines the averaging process, particularly for large data sets. The downside is the potential for input errors and a small learning curve for those unfamiliar with such software.

Utilizing Online Calculators

Many online calculators can compute average percentages at the click of a button, ideal for quick calculations without any hassle.

Steps:

1. Find a reliable online calculator: Search for an online average percentage calculator using a search engine.
2. Input your percentages: Enter your percentages into the calculator’s designated fields.
3. Click ‘Calculate’: By clicking on the calculate or equivalent button, the calculator will provide the average.
4. Review the result: Ensure the result displayed by the calculator makes sense in context.

Summary:

Online calculators are convenient and user-friendly. However, relying on online tools requires caution, as incorrect inputs will lead to inaccurate results, and the availability of an internet connection is necessary.

Understanding Percentages through Visualization

For those who are visual learners, creating charts or graphs can be a valuable way to understand percentages and their averages.

Steps:

1. Collect your percentages: Have your list of percentages ready.
2. Choose a method of visualization: Decide whether a pie chart, bar graph, or another visual representation would best help you grasp the information.
3. Create your visualization: Use a spreadsheet program or a dedicated chart-making tool to create your chart or graph.
4. Calculate average graphically: Use the visual cues from the chart to estimate or calculate the average percentage.

Summary:

Visualization methods can offer a clearer big-picture view of percentages and their interrelations. However, this approach may not always provide the precision necessary for exact calculations.

Progressive Averaging Approach

When calculating averages sequentially, such as adding new percentage values over time, the progressive averaging approach is useful for continually updating the average.

Steps:

1. Start with your initial average: Identify the starting average percentage if one exists.
2. Incorporate new percentage: Add the new percentage to the existing average considering its weight.
3. Calculate the new average: Adjust the average to account for the new percentage.
4. Repeat as needed: Continuously repeat this process as new percentages are added over time.

Summary:

The advantage of progressive averaging is its dynamism and adaptability to a changing dataset. It is especially useful in ongoing processes or when data arrives incrementally. However, it may be less efficient for larger, static datasets.

Understanding Decimal Conversions

Converting percentages to decimals can simplify the averaging process, especially if you’re working with non-whole numbers.

Steps:

1. Convert percentages to decimals: Divide each percentage by 100.
2. Average the decimals: Add the decimal values together and divide by the number of values to find the average.
3. Convert back to a percentage: Multiply the average decimal by 100 to get the average percentage.

Summary:

This method can simplify mental calculations and can sometimes reveal more nuances in the data. But, it adds an extra step which can potentially introduce errors in the conversion process.

Avoiding Common Mistakes

When calculating average percentages, certain pitfalls can lead to incorrect results. Being aware of common mistakes improves accuracy.

Tips and Tricks:

• Double-check your inputs: Ensure all entered percentages are correct.
• Watch for outliers: Be wary of unusually high or low percentages that can skew the average.
• Use precise values: Round off the final average, not the individual percentages.

Summary:

Avoiding common mistakes can significantly enhance the accuracy of your calculations. Meticulous attention to detail is key, but this can be time-consuming and may require practice to master.

Practical Application through Examples

Applying your knowledge to practical examples can solidify your understanding of calculating average percentages.

Steps:

1. Create sample scenarios: Draft realistic situations where average percentages would be required.
2. Perform the calculations: Use the methods mentioned earlier to calculate the averages within these examples.
3. Analyze the results: Review the averages, considering the context of each scenario.

Summary:

Practical examples cement theoretical knowledge and demonstrate the relevance of average percentage calculations in daily life. On the downside, hypothetical examples may not cover all real-life complexities and variations.

Fostering Mental Math Skills

Developing mental math strategies can be empowering and practical, enabling quick average percentage estimations without the need for calculators or tools.

Tips and Tricks:

• Practice rounding: Round percentages to the nearest whole number for faster mental calculations.
• Learn basic percentages: Familiarize yourself with common percentage-to-decimal conversions to speed up the process.
• Estimate averages: Use logical estimates to get a rough average when precision is not critical.

Summary:

Mental math enhances speed and convenience in calculating averages. However, estimations may lack precision, which is sometimes necessary in more formal or exacting contexts.

In conclusion, calculating average percentages need not be a daunting task. With the right approach—be it through traditional means, technological tools, or mental strategies—you’ll find that arriving at an accurate average can be both satisfying and revealing. It’s a skill that, once mastered, enables better decision-making in diverse aspects of work and life.

Frequently Asked Questions:

1. Can I use the traditional averaging method when each percentage carries a different value or weight?

   • No, the traditional averaging method assumes each percentage has equal value. If the percentages have different weights, you should use the weighted average technique.

2. How accurate are online average percentage calculators?

   • Online calculators are as accurate as the data entered into them. They are programmed to calculate averages correctly, but any input errors will result in the wrong average.

3. What should I do if my dataset is too large to calculate averages manually?

   • For large datasets, it’s most efficient to use a spreadsheet program like Excel, which can handle large amounts of data quickly and minimize the potential for human error.