In the world of science, particularly chemistry, understanding the relationship between different units of measurement is crucial. One common challenge faced by students and professionals alike is converting milliliters (mL), a unit of volume, to moles (mol), a unit of substance amount. This process is key to many laboratory procedures and calculations in chemistry. It involves understanding the concept of molarity, the density of the substance, and its molecular weight. With a step-by-step approach and clear explanations, this guide is designed to simplify the conversion process for those who may not be familiar with the technical details of chemical measurements.
Converting Using Molarity
When you have a solution of a known concentration (molarity), calculating moles from milliliters becomes straightforward.
Detailed Introduction
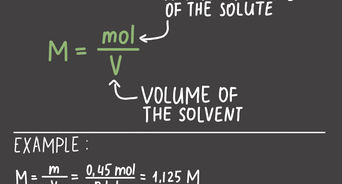
Molarity is a measure of the concentration of a solute in a solution. It is defined as the number of moles of solute divided by the liters of solution. This method is useful when you are dealing with liquid solutions where the concentration is given in molarity (M).
Detailed Steps
-
Identify the concentration: Find the molarity of your solution, usually listed on the container or provided in your experiment.
-
Measure the volume: Determine the volume in milliliters (mL) of your solution that you are working with.
-
Convert mL to L: Since molarity is moles per liter, you need to convert your volume from milliliters to liters by dividing by 1000.
-
Calculate moles: Multiply the volume in liters by the molarity to obtain the number of moles.
For example, if you have 50 mL of a 2 M solution, first convert 50 mL to 0.05 L, then multiply by 2 M to get 0.1 moles.
Summary
This approach is reliable and quick, ideal for aqueous solutions with a known molar concentration. However, it assumes the molarity is accurate, which might not be the case if the solution has degraded or been contaminated.
Using Density and Molar Mass
For pure substances with known density, calculating moles from milliliters involves using the substance’s density and its molar mass.
Detailed Introduction
The density of a substance links its volume and mass. By using the known density and molar mass, you can calculate the number of moles contained in a given volume of liquid substance.
Detailed Steps
-
Find the density: Obtain the density of the substance in grams per milliliter (g/mL).
-
Measure the volume: Record the volume of the substance in milliliters.
-
Determine the mass: Multiply the volume by the density to find the mass in grams.
-
Identify the molar mass: Find the molar mass of the substance, typically listed on its molecular formula or a periodic table, in grams per mole (g/mol).
-
Calculate moles: Divide the mass by the molar mass to find the number of moles.
For example, if you have 20 mL of ethanol with a density of 0.789 g/mL and a molar mass of 46.068 g/mol, the mass is 20 mL x 0.789 g/mL = 15.78 g. Then divide the mass by the molar mass: 15.78 g / 46.068 g/mol = 0.342 moles.
Summary
This method provides a precise calculation for pure substances, but it demands accuracy in measuring the density and molar mass. The downside is that certain substances’ densities can vary with temperature and purity.
Using Dilution Equations
Dilution equations allow the calculation of moles from milliliters when diluting a concentrated solution.
Detailed Introduction
A dilution occurs when you add a solvent to a solution, reducing the solute’s concentration. The moles of solute remain constant before and after the dilution, which can help in determining the number of moles in a new volume.
Detailed Steps
-
Understand the dilution equation: The equation C1V1 = C2V2, where C represents concentration and V volume, relates the initial and final states of the dilution.
-
Record initial concentration and volume: Determine or note the concentration (C1) and volume (V1) before dilution.
-
Record final concentration and volume: Measure or calculate the new concentration (C2) and volume (V2) after dilution.
-
Use the equation to find moles: Rearrange the equation to solve for the initial moles (C1V1) or use the final moles (C2V2) if more convenient, keeping in mind that they are equal.
For example, if you start with 100 mL of a 1.5 M solution and dilute it to 500 mL, the number of moles in both solutions remains the same. Therefore, 1.5 M × 0.1 L = C2 × 0.5 L. Solving for C2 gives you 0.3 M, which indicates that there were initially 0.15 moles in the 100 mL solution.
Summary
Dilution equations are powerful for handling concentration changes without directly measuring moles. The limitation, however, is that they rely on precise initial measurements of concentration and volume.
Using Percent Composition
Sometimes you may need to calculate moles from milliliters using the percent composition by volume in mixtures.
Detailed Introduction
Percent composition by volume is the percentage of a solution that one substance makes up. This knowledge, combined with the total volume and the density of the pure substance, allows the determination of moles of that substance.
Detailed Steps
- Determine percent composition: Find the percent composition by volume of the substance in your mixture.
- Measure the total volume: Obtain the total volume of the mixture you have.
- Calculate the volume of interest: Multiply the percent composition by the total volume to find the volume of the substance you’re interested in.
- Convert to mass using density: Use the density of the pure substance to convert this volume to mass.
- Find moles from the mass: Finally, use the molar mass of the substance as described in previous methods to calculate the number of moles from the mass.
Summary
This method is useful for mixtures and solutions where one component’s volume percentage is known. The challenge lies in ensuring the percent composition and the density are precise and applicable to the specific conditions (like temperature) of the mixture.
Using Ideal Gas Law
If dealing with a gas at known conditions of temperature and pressure, you can calculate moles from milliliters using the Ideal Gas Law.
Detailed Introduction
The Ideal Gas Law, PV = nRT, relates pressure §, volume (V), moles of gas (n), the universal gas constant ?, and temperature (T). With known volume, temperature, and pressure, you can calculate the number of moles.
Detailed Steps
-
Record the pressure: Note the pressure at which your gas is measured.
-
Measure the volume: Convert the volume from mL to liters, as the gas constant is typically given in liters.
-
Record temperature: Temperature must be in Kelvin for the ideal gas equation.
-
Know the gas constant ?: R = 0.0821 Latm/molK or the equivalent in other units depending on your pressure measurement.
-
Calculate moles: Rearrange the ideal gas law to solve for n (moles) and insert your known values to calculate.
For example, for a 500 mL sample of gas at 1 atm and 300 K, first convert the volume to 0.5 L. Using the ideal gas constant, rearrange the equation to n = PV / RT, and calculate n as (1 atm × 0.5 L) / (0.0821 Latm/molK × 300 K), which gives you approximately 0.0203 moles.
Summary
The Ideal Gas Law provides a robust way to calculate moles for gases under various conditions. Its precision depends on how closely the gas follows ideal behavior, which can vary with extreme temperatures or pressures.
Estimating with Rule of Thumb
There are some general ‘rules of thumb’ that can simplify calculations, such as using 1 mL = 1 cm.
Detailed Introduction
Sometimes, you don’t need an extremely precise number of moles, or you just need an estimate to start with. Simple rules of thumb, based on approximations or common substance properties, can be useful here.
Detailed Steps
- Know your substance: Certain liquids have a density close to that of water, 1 g/mL (e.g., dilute aqueous solutions).
- Use the 1 mL = 1 cm approximation: This helps to visualize the amount of substance you’re dealing with.
- Estimate moles for water-like densities: If dealing with such a substance, estimate 1 mL as 1 g and use the molar mass to find a rough number of moles.
Summary
Rules of thumb provide a fast, ballpark figure which is helpful for quick checks or crafting hypotheses. They are not accurate for precise calculations or substances with densities significantly different from water.
Dilution Factor Calculation
Dilution factor is another method to determine moles from milliliters, particularly for serial dilutions.
Detailed Introduction
The dilution factor is the ratio of the initial and final concentrations of a solution and is especially useful when performing a series of dilutions, a common practice in biology and chemistry labs.
Detailed Steps
- Understand dilution factor: It’s typically written as 1:X, where X is the factor by which the concentration decreases.
- Find initial concentration: Determine the molarity of the original solution.
- Calculate the dilution factor: If you know the volumes of the solute and the solvent added, the dilution factor is (solute volume + solvent volume) / solute volume.
- Calculate the final concentration: Divide the initial concentration by the dilution factor to get the final concentration.
- Find moles from mL: Use the final concentration and volume as mentioned in previous methods to calculate the number of moles.
Summary
This calculation is particularly useful for labs where solutions are often diluted. However, errors can accumulate over a series of dilutions, leading to less accurate results.
Stoichiometry Method
Stoichiometry is the method of calculating relative quantities of reactants and products in chemical reactions.
Detailed Introduction
In stoichiometry, one starts with a balanced chemical equation and uses the relationship between the reactants and products to calculate moles.
Detailed Steps
- Balance the equation: Ensure the chemical equation is balanced.
- Identify the reactant or product of interest: Decide which substance’s moles you want to calculate.
- Find the volume to mole ratio: Use the molarity or percent composition methods previously discussed, if applicable.
- Convert using stoichiometry: Apply the mole ratio from the balanced equation to convert from moles of one substance to another.
Summary
Stoichiometry is a cornerstone of chemistry calculations, allowing for precise mole calculations in reactions. The process requires a solid understanding of chemical reactions and may not be straightforward for complex reactions.
Hydration Method
When dealing with hydrates – compounds that include water molecules as part of their structure – a specific method is used to calculate moles from milliliters.
Detailed Introduction
Hydrates are solid compounds that have a specific number of water molecules bound within their crystal structure. To find the number of moles in a given volume, you need to consider the combined molar mass of the compound and its waters of hydration.
Detailed Steps
- Identify hydrate and chemical formula: Determine the chemical formula, including the waters of hydration (e.g., CuSO4·5H2O).
- Find combined molar mass: Add the molar mass of the anhydrous compound to the molar masses of the water molecules.
- Calculate moles as before: Use the density and the combined molar mass, as discussed in previous methods, to calculate moles.
Summary
The hydration method is essential for calculating moles in hydrates accurately. It requires additional steps to account for the water in the substance’s structure, which can be a source of error if overlooked.
Empirical and Molecular Formula Conversion
When you have the empirical or molecular formula of a substance, you can convert milliliters to moles by calculating the molar mass.
Detailed Introduction
The empirical formula represents the simplest whole-number ratio of elements in a compound, while the molecular formula is the actual number of each type of atom in the molecule. Both can be used to find the molar mass, which is crucial for converting mL to moles.
Detailed Steps
- Understand formula type: Identify whether you’re working with an empirical or molecular formula.
- Calculate molar mass: Use the periodic table to find the atomic mass of each element and multiply by the number of atoms indicated in the formula.
- Convert volume to mass using density: Calculate mass from mL as previously described.
- Calculate moles using molar mass: Divide the mass by the molar mass to find moles.
Summary
The formulas provide a clear pathway to calculating moles, especially with pure substances. The potential downside is the necessity to ensure the correct formula type and calculation of molar mass, which can sometimes be complex for larger molecules.
Conclusion
Understanding how to calculate moles from milliliters involves a blend of fundamental concepts from chemistry and a variety of techniques suited to different scenarios. Whether working with solutions, pure substances, gases, or even participating in chemical reactions, the methods provided offer a comprehensive toolkit to tackle this challenge. It’s important to choose the correct method based on the information available and the nature of the substance being measured. With practice, patience, and attention to detail, anyone can master the art of these conversions.
FAQs
-
What is molarity and how does it relate to calculating moles?
Molarity is a measure of the concentration of a solution, typically expressed as moles of solute per liter of solution. It directly relates the volume of a solution to the number of moles contained in that volume. -
Why do I need to know the density of a substance to calculate moles from milliliters?
Density links volume and mass. To calculate moles, one often needs to first find the mass of substance in a given volume, which requires the knowledge of its density. -
Can I calculate the number of moles from mL if I only know the percentage composition by volume?
Yes, by knowing the percentage composition by volume and the total volume of the mixture, you can calculate the volume (and hence mass and moles) of the substance of interest. -
What is the ideal gas law and how does it help in calculating moles from milliliters?
The Ideal Gas Law is PV = nRT, where P is pressure, V is volume, n is moles, R is the universal gas constant, and T is temperature in Kelvin. It helps calculate the number of moles of a gas when the other conditions (P, V, T) are known. -
Is there a simple way to estimate moles from milliliters without complex calculations?
Yes, for substances with a density similar to water, you can estimate 1 mL as 1 gram and then divide by the molar mass to get an approximate mole value.