How to Calculate Volume From Mass and Density

Calculating the volume of an object when its mass and density are given might initially seem challenging. However, understanding volume, mass, and density and how they relate to each other is quite straightforward with some guidance. Volume is the amount of space that an object occupies, mass is the amount of matter in the object, and density is the mass per unit of volume. The relationship between them is a fundamental concept in physics and engineering, and learning to calculate one from the others is a useful skill. With a few simple mathematical steps, you can accurately determine an object’s volume—whether it’s a liquid in a jug or a metal block on your workbench.

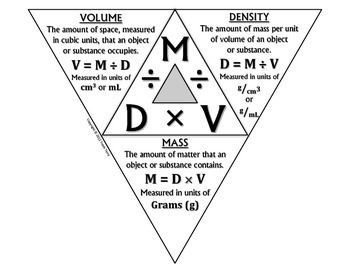
Using Basic Formula

If an object has a constant density and a uniform shape, you can use a simple formula to calculate its volume. Here’s how it works:

Detailed Steps:

1. Write down the formula: Volume = Mass ÷ Density. This formula comes from the definition of density, which is mass per unit volume.

2. Measure the mass of the object using a balance or scale. Ensure the unit of mass is in kilograms (kg) or another unit that matches the density’s unit.

3. Obtain the density of the substance. This information can be found in reference materials or online databases. Density should be in units compatible with the mass (for example, kilograms per cubic meter, or kg/m).

4. Divide the mass of the object by the density to find the volume. For example, if the mass is 10 kg and the density is 2 kg/m, the volume would be 10 kg ÷ 2 kg/m = 5 m.

Summary:

This method is straightforward and highly accurate for objects with uniform density. However, it doesn’t account for variations in density that may exist in non-uniform objects.

Water Displacement Method

For irregularly-shaped objects or those with non-uniform density, the water displacement method is a more practical approach.

Detailed Steps:

1. Fill a graduated cylinder or overflow can with water. Note the initial volume level of the water without the object.

2. Gently submerge the object into the water. Ensure the object is completely covered by the water.

3. Record the new volume level of the water with the object submerged.

4. Subtract the initial volume from the new volume to find out the volume of the object.

Summary:

The water displacement method is great for irregular objects where direct volume calculation is not possible. Its downside is the potential mess and inaccuracy with soluble or water-damaged objects.

Using Dimension Measurements

For regular solid objects, such as cubes or spheres, direct measurement of dimensions and applying geometrical formulas can calculate volume.

Detailed Steps:

1. Measure the object’s dimensions—length, width, and height for a cube, or the radius for a sphere, etc.

2. Write down the appropriate volume formula for the object’s shape (e.g., Volume of a cube = side).

3. Plug the dimension measurements into the formula and solve for the volume.

Summary:

This method provides a direct and generally accurate volume calculation for geometrically regular objects. However, it can be complex for objects with complicated shapes and is impractical for those whose geometry is unknown or inconsistent.

Using Archimedes’ Principle

Archimedes’ Principle can be applied for objects that can be submerged in water without damage, especially if the object is heavier and would sink in water.

Detailed Steps:

1. Use a scale to measure and record the weight of the object in air.

2. Fill a container with water to a point that allows the full submersion of the object without overflow.

3. Submerge the object attached to a string and measure the weight while submerged.

4. The difference in weights is equal to the weight of the water displaced. Use the density of water to find the volume of water displaced, which equals the volume of the object.

Summary:

This technique is helpful for complex shapes and densities. However, it requires precision in measurement and is not suitable for water-soluble or absorbent materials.

Density Tables

Sometimes, the density of an object is difficult to ascertain, but with density tables, you can work backward to find volume if you know the material and mass.

Detailed Steps:

1. Identify the material of the object.

2. Look up the material’s density in a density table.

3. Use the density and mass of the object in the volume formula to calculate the volume.

Summary:

Density tables provide an easy and quick reference but are contingent on the accuracy of the mass measurement and the assumption that the material is pure and of uniform density.

Using a Scale for Liquids

Liquids assume the shape of their container but do not have a uniform size or shape, so a scale can be used to measure their volume indirectly when their density is known.

Detailed Steps:

1. Weigh the container with the liquid and then without it to find the mass of the liquid itself.

2. Consult a reference for the liquid’s density at the temperature of measurement.

3. Use the volume formula to calculate the liquid’s volume.

Summary:

This is a precise method for liquid volume measurements, but its accuracy depends on knowing the exact density at the measurement temperature.

CAD Modelling Software

For objects designed in CAD (Computer-Aided Design) software, volume can often be calculated automatically.

Detailed Steps:

1. Create or open the 3D model of the object in the CAD software.

2. Locate the software’s volume calculation tool.

3. Select the object for which you need the volume and allow the software to calculate it.

Summary:

CAD volume calculations are exact for the model dimensions but don’t account for manufacturing variances or material densities unless specified.

Using a 3D Scanner

With 3D scanning technology, you can obtain a model of an object which can then be used to calculate volume.

Detailed Steps:

1. Scan the object using a 3D scanner following the manufacturer’s instructions.

2. Import the scan data into a suitable software that can calculate volumes.

3. Use the software to calculate the volume of the scanned object automatically.

Summary:

3D scanning is helpful for complex and irregularly shaped objects but requires expensive equipment and might introduce errors based on the scanner’s resolution.

Specific Gravity Method

If you know the specific gravity of a substance, you can calculate its volume from mass without actual density values.

Detailed Steps:

1. Weigh the object to determine its mass.

2. Obtain the specific gravity of the substance, which is a ratio comparing its density to that of water.

3. Since the density of water is 1 g/cm or 1000 kg/m at 4°C, multiply the specific gravity by the density of water to get the density of your substance.

4. Calculate the volume using the volume formula.

Summary:

The specific gravity method is simple and effective for quick estimates but requires the assumption that the specific gravity values are correct and that temperature effects on density are negligible.

Experimentation and Iteration

When all else fails, sometimes experimenting with different methods and iterating can lead to an accurate volume calculation.

Detailed Steps:

1. Estimate the volume using various methods detailed above.

2. Record all results and compare them for consistency and accuracy.

3. Identify the method that provides the most consistent results and refine the technique as needed for precision.

Summary:

Experimentation is time-consuming and requires patience but can yield accurate results when standard methods fail or when dealing with highly irregular objects.

In conclusion, calculating the volume from mass and density involves understanding the relationship between these physical properties. There are various methods available, ranging from mathematical calculations to practical experiments. Each method has its own benefits and potential downsides, which are often related to the type of object being measured and the conditions under which the measurements are taken. By considering these factors, you can choose the most appropriate method to obtain accurate volume measurements.

FAQs:

1. What if my object has a non-uniform density, can I still calculate the volume using the mass and density?

   • Yes, you can calculate an average volume using the mass and average density, but for precise measurements, consider using methods tailored to non-uniform objects, like water displacement or Archimedes’ principle.

2. Can I calculate the volume of an oddly-shaped object using these methods?

   • For irregular shapes, water displacement or 3D scanning methods work best as they do not rely on predefined geometrical formulas.

3. Is it necessary to have the temperature the same when measuring mass and density for a liquid?

   • Yes, the temperature can significantly affect the density of a liquid, so it is important to measure both at the same temperature for accurate volume calculations.