How to Calculate 2 3 of a Number

Navigating the world of math can often seem like an endless labyrinth of numbers and equations, but fear not! Understanding how to calculate fractions of a number is a practical and essential skill that can simplify many aspects of life, from cooking to budgeting. With a dash of patience and a spoonful of clarity, the process of finding two-thirds of any number can become second nature. Let’s embark on an arithmetic adventure that will open up new possibilities and sharpen your calculating capabilities.

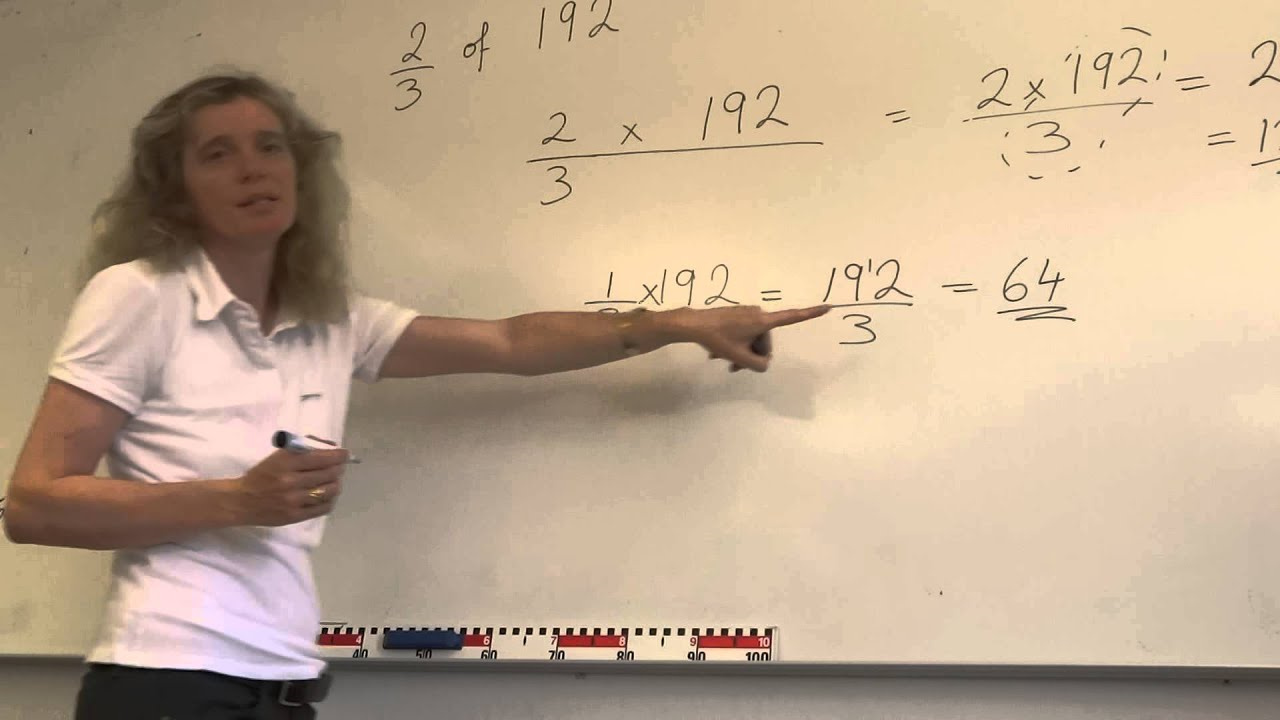
Traditional Fraction Multiplication

To find two-thirds of a number, envision it as sharing a pie – you want to divide it into three equal parts and take two. This visualization aligns perfectly with the mathematical approach, where you multiply the number by the fraction.

Detailed Introduction

Traditional fraction multiplication is a straightforward method that involves multiplying the whole number by the numerator of the fraction and then dividing the product by the denominator. In the case of finding two-thirds, the numerator is 2 and the denominator is 3.

Detailed Steps

1. Identify the whole number you wish to find two-thirds of.
2. Multiply this number by 2, which is the numerator of the fraction “two-thirds.”
3. Take the result from step 2 and divide it by 3, which is the denominator of the fraction.
4. The result from step 3 is two-thirds of the original number.

Summary

This traditional method is beneficial due to its simplicity and wide applicability. However, for those who struggle with multiplication and division, it might present a challenge.

Decimal Conversion

Turn the fraction into a decimal to streamline the multiplication process, creating a less intimidating approach for those who prefer working with decimal numbers.

Detailed Introduction

Converting two-thirds to a decimal gives you approximately 0.6667 (rounded to four decimal places). Multiplying any number by this decimal should result in the same answer as using the traditional fraction method.

Detailed Steps

1. Remember or look up that two-thirds as a decimal is approximately 0.6667.
2. Multiply the whole number you’re working with by 0.6667.
3. Round the result to the desired number of decimal places.

Summary

The decimal method is quick and often more intuitive for people comfortable with decimal multiplication. However, it introduces a small margin of error due to rounding the decimal equivalent of 2/3.

Percent Conversion

Think of the fraction as a part of 100 to bring it into the realm of percentages, which can often be easier to understand and calculate.

Detailed Introduction

Converting two-thirds into a percent gives you around 66.67%. This transformation allows using a percent-based approach for calculation, which can be particularly handy when dealing with discounts or financial figures.

Detailed Steps

1. Understand that two-thirds is equivalent to roughly 66.67%.
2. Convert the whole number into a percentage by keeping it as is (since any number is 100% of itself).
3. Multiply the original number by 66.67% (or 0.6667 in decimal form).
4. The product will be two-thirds of the original number, expressed either as a decimal or a whole number.

Summary

Using percentages can make calculations feel more relatable and practical, especially in real-world contexts. However, precision may be slightly compromised due to the necessity of rounding the percentage.

Ratio Understanding

Consider the part-to-whole relationship of the fraction, which can be helpful in understanding proportional relationships.

Detailed Introduction

Viewing two-thirds in terms of ratios — 2 parts taken out of every 3 parts — helps to conceptualize what fraction of the whole is being dealt with. This can assist in visualizing the division and multiplication process.

Detailed Steps

1. Envision the number as split into three equal parts.
2. Understand that taking two parts out of these three gives you the ratio of 2:3.
3. Multiply the original number by 2 and then divide it by 3 to maintain this ratio.
4. The result is two-thirds of the initial number, reflecting the 2:3 ratio.

Summary

Ratios make it easier to visualize problems and can be particularly user-friendly for visual learners. The primary disadvantage is that it might not be as quick as direct multiplication or using decimals.

Using a Calculator

Utilize digital tools to calculate two-thirds of a number quickly and efficiently.

Detailed Introduction

In an era where technology is at our fingertips, using a calculator to find two-thirds of any number is a convenient option. This approach minimizes the potential for error and speeds up the process.

Detailed Steps

1. Input the number you need to calculate two-thirds of into the calculator.
2. Press the multiplication button (usually marked as x or *).
3. Type in 0.6667 (the decimal form of 2/3) or (2/3) if your calculator has a fraction feature.
4. Press the equal button (=) to obtain the result.
5. The displayed number is two-thirds of the original figure.

Summary

The calculator method is fast and reduces manual calculation errors, making it ideal for those less comfortable with math. However, it may not improve your mental math skills and can be less satisfying for those who enjoy the process of calculating by hand.

Proportional Model

Scale up or down from a known two-thirds value by using proportions.

Detailed Introduction

If you know two-thirds of a certain number, you can find two-thirds of another number by establishing a proportion and scaling accordingly. This method is effective when you can easily relate the new number to one you’re already familiar with.

Detailed Steps

1. Identify a number whose two-thirds value you know.
2. Determine the proportion between the new number and the known number.
3. Scale the known two-thirds value by this proportion to find the two-thirds of the new number.
4. Verify this result by doing a traditional calculation.

Summary

The proportional model is a powerful tool for comparing relative sizes and making quick estimates. Its disadvantage lies in the initial requirement of having a known two-thirds value to act as a reference.

Unfortunately, there aren’t ten distinct solutions for calculating two-thirds of a number, as the mathematical operation is quite straightforward. However, here are some tips and tricks that can further assist in understanding and performing this calculation:

Tips and Tricks

Visual Aids

Use pie charts or bar models to visually divide a number into thirds and then count two of those parts. This can be especially helpful for those who learn best with visual support.

Practice with Whole Numbers

Start by practicing with whole numbers that are divisible by 3. This can build your confidence before moving on to more complex numbers.

Fractional Blocks

Fraction blocks or online interactive tools can offer a hands-on approach to learning fractions and their equivalents, which can be more engaging and informative.

Common Fractions Sheet

Keep a reference sheet with common fractions and their decimal and percent equivalents handy. This can expedite the process and reinforce learning.

Real-world Application

Apply the concept of calculating two-thirds to real-life situations, like splitting a bill or dividing a recipe, to enhance understanding and retention.

Online Fraction Calculators

Online calculators specifically designed for fraction operations can be a great resource when you’re unsure about your calculations.

Conclusion

Calculating two-thirds of a number doesn’t have to be an onerous task. With a variety of methods and tools at your disposal, you can choose the one that best suits your comfort level and needs. Whether you prefer the straightforwardness of traditional multiplication, the modern convenience of digital calculators, or the visual appeal of proportional models, becoming adept at this calculation can save you time and effort in many practical situations. Keep practicing, and soon this fraction-finding process will be as natural to you as breathing.

FAQs

1. Why do we round two-thirds to 0.6667 when converting to a decimal?

   • Two-thirds is a repeating decimal (0.6666…), and for practical purposes, it must be rounded to a finite number of decimal places. 0.6667 is commonly used because it rounds up the last digit, offering a slightly more accurate representation.

2. Can I use these methods to calculate other fractions of a number?

   • Absolutely! The methods described can be applied to calculate any fraction of a number. Simply substitute the appropriate numerator and denominator where applicable.

3. What if the number I’m working with is already a decimal?

   • You can still use any of these methods if the number is a decimal. For instance, using a calculator will work the same way as with whole numbers, and for the traditional method, you would perform the multiplication and division as you normally would with decimal values.