When we think about measuring spaces, we often imagine measuring a room, which usually has a rectangular shape. However, sometimes you might find yourself needing to measure an area with a very different shape: the triangular one. Whether you’re laying new carpet, planting a garden, or calculating the area of a triangular parcel of land, knowing how to determine the square footage of a triangle is a handy skill. The process is straightforward once you understand the basic geometry formulas involved. Here’s your guide to doing just that, broken down into approachable methods and some useful tips.
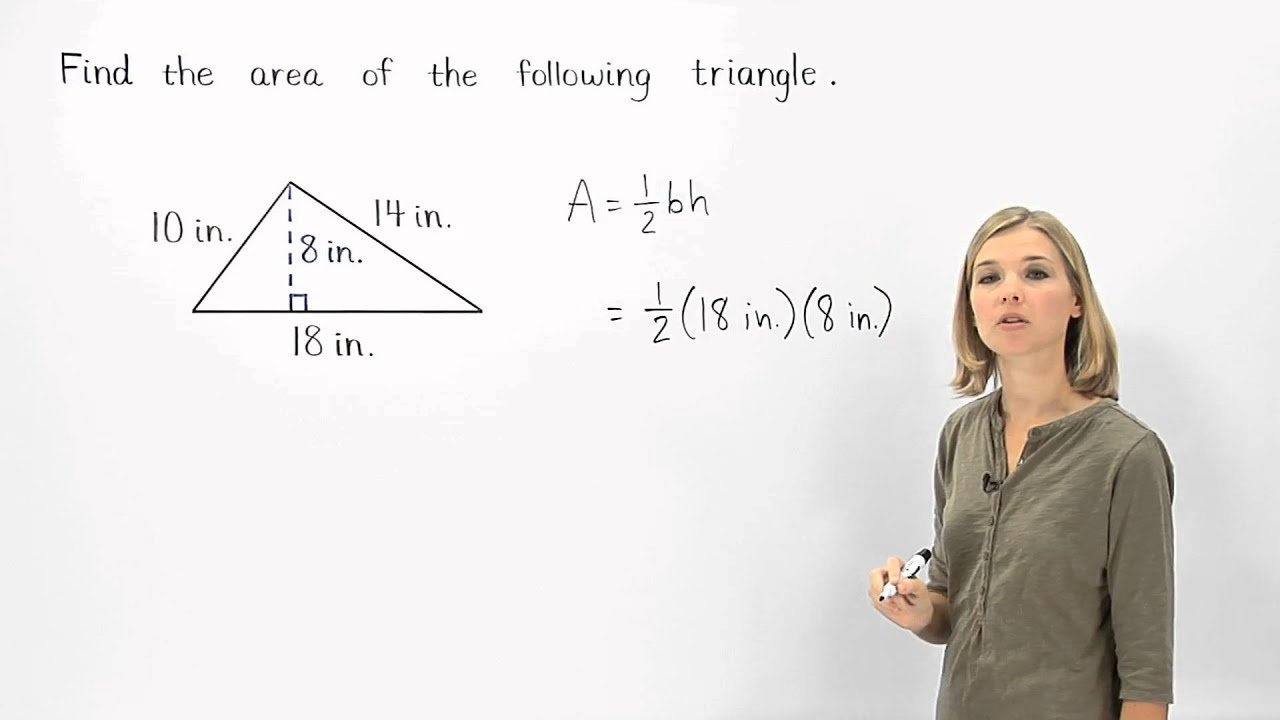
Basic Triangle Area Calculation
To calculate the square footage of a triangle, the most commonly used method is applying the basic formula that uses the base and the height of the triangle.
Detailed Introduction
Every triangle has a base (the bottom side) and a height (the perpendicular line from the base to the top point). To get the square footage, you multiply those two numbers together and halve the result.
Detailed Steps
- Measure the length of the base of the triangle.
- Measure the height, ensuring that it is perpendicular to the base.
- Multiply the base length by the height.
- Divide the product by two to get the square footage.
Summary
This method is straightforward and effective for any right-angled or equilateral triangle where height can be easily measured. However, it could be less convenient for obtuse or acute triangles where determining the height isn’t as clear-cut.
Heron’s Formula for Irregular Triangles
When you don’t have a right angle in your triangle, Heron’s formula comes to the rescue as long as you know the length of all three sides.
Detailed Introduction
Heron’s formula allows you to calculate the area of a triangle when you know the lengths of all three sides. It uses the semi-perimeter (half of the total perimeter) in its calculation.
Detailed Steps
- Measure all three sides of the triangle.
- Calculate the semi-perimeter by adding all three side lengths together and dividing by two.
- Subtract the length of each side from the semi-perimeter, and multiply these three results together with the semi-perimeter.
- Take the square root of the product to find the area in square units.
Summary
Heron’s formula is great for irregular triangles, but it requires accurate measurements of all sides and can involve more complex calculations.
Using a Grid to Estimate Area
In scenarios where precise measurements are challenging, you can estimate the area of a triangle using a grid overlay method.
Detailed Introduction
By overlaying a grid of equal squares (like graph paper) over the triangle, you can count the full squares within the triangle and do a rough estimate of the partial ones to determine the area.
Detailed Steps
- Place a grid over the triangle or draw one on it.
- Count the full squares within the triangle.
- Estimate the total area of the partial squares.
- Add the areas of full and partial squares to estimate the total area.
Summary
This method is quick and doesn’t require complex formulas, but it’s an estimate and not precise for exact calculations.
Other Tips and Tricks
The Pythagorean Theorem
Useful for right-angled triangles, to calculate the missing side if you only know two sides, which can then help with area calculations using the basic formula.
Trigonometric Methods
Involves using sine, cosine, and tangent functions to find missing sides or angles, which could then facilitate the use of other area calculating methods.
Surveyor’s Formula
For larger triangular plots, the Surveyor’s formula can be a helpful tool, using latitude and longitude or surveyed boundaries to calculate area.
Software Solutions
Geometric design software can calculate areas for you with just a few clicks, as long as you can input the necessary measurements or angles.
Photogrammetry for Large Areas
Using photographs and software to calculate the area of very large triangles, like land plots or lots.
Consulting a Professional
For areas where precise calculation is crucial, consulting a surveyor or a professional might be the best solution to ensure accuracy.
Importance of Accuracy
Be sure to double-check measurements and calculations, as errors can lead to significant discrepancies in area estimation.
Real-Life Applications
Understanding calculations also applies in real scenarios, such as real estate, construction, or landscaping projects.
Laws and Regulations
Always consider local laws and regulations when measuring property-related triangles, as there might be specific requirements or methods that are legally recognized.
In conclusion, knowing how to calculate the square footage of a triangle is a valuable skill that can come in handy in various practical situations. Whether you’re planning a garden layout, working out the size of a piece of land, or simply tackling a DIY project, having multiple methods at your disposal means you can adapt to the shape and specifics of any triangle you encounter. While some approaches are more precise than others, it’s important to choose the right one for your needs, and not to shy away from seeking professional help when accuracy is paramount.
FAQs
-
Do I always need to use mathematics to calculate the square footage of a triangle?
Yes, mathematical formulas are generally required to accurately determine the area of a triangle. However, for rough estimates, less mathematical methods such as the grid method can be used. -
Can I calculate the square footage if I only know the length of one side and one angle?
To calculate the area, you typically need more information. With one side and one angle, you might use trigonometric methods to find other sides or heights if the triangle includes a right angle, but you would usually need at least one additional measurement or angle. -
What’s the most accurate way to calculate the square footage of a triangle?
The most accurate method depends on the type of triangle and the available information. For right-angled triangles, the base times height divided by two is very accurate. For non-right-angled triangles, if you know all sides, Heron’s formula is effective. For maximum precision, especially with large land areas, hiring a professional surveyor is recommended.