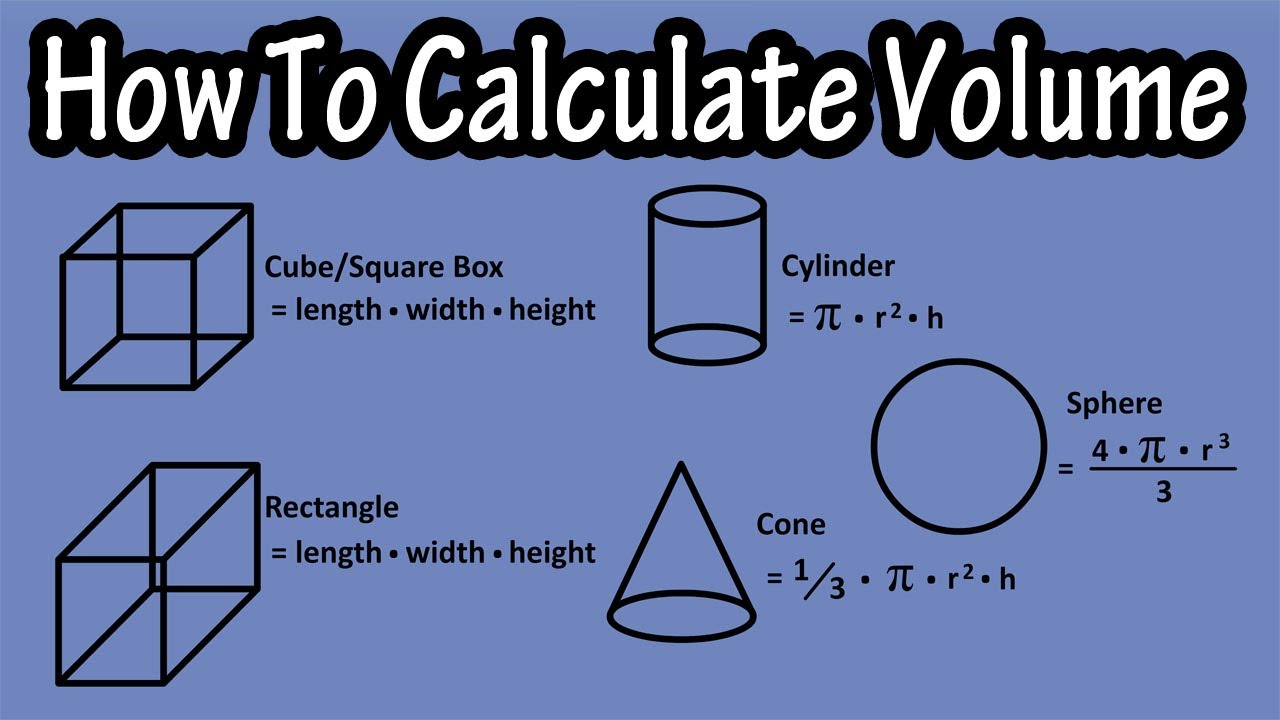
When we consider shapes and geometric figures, we often think of simple dimensions like length and width. But when we enter the realm of three-dimensional shapes, volume becomes a crucial measurement. The volume of an object tells us how much space it occupies, and understanding how to calculate it can be essential, especially in fields such as construction, manufacturing, and science. For circular objects, which are typically part of cylinders or spheres, volume calculations can initially seem daunting. However, by breaking down these calculations into clear, manageable steps, anyone can confidently determine the volume of circular shapes.
Using Cylinder Volume Formula
The volume of a circle is usually sought within the context of cylinders because circles themselves are two-dimensional and do not have a volume. The cylinder is a three-dimensional shape that extends a circle along another dimension—height. To find out how much space a cylindrical object occupies, you can use the simple mathematical formula for volume.
Detailed Steps:
- Start by measuring the radius of the circular base of the cylinder. This can be done by measuring the distance from the center of the circle to its edge.
- Next, measure the height of the cylinder, which is the distance from one circular base to the other.
- Use the formula for the volume of a cylinder: V = πrh, where V is volume, π (pi) approximately equals 3.14159, r is the radius of the circle, and h is the height of the cylinder.
- Square the radius by multiplying it by itself.
- Multiply this result by the height of the cylinder.
- Finally, multiply the product of the radius squared and height by π to get the volume.
Summary:
Calculating the volume using the cylinder formula is straightforward and provides an accurate measurement of space occupied by a cylindrical object. It is essential in many practical applications. However, a potential downside is that if the measurements are not accurate, the calculated volume will be incorrect.
Estimating with a Ruler
Sometimes precision tools aren’t available, and an estimate of volume is sufficient. Using a ruler, even if not perfectly precise, can give you a ballpark figure that can be useful in everyday situations.
Detailed Steps:
- Use the ruler to measure the diameter of the circular base of the cylinder as accurately as possible.
- Divide the diameter by two to find the approximate radius.
- Measure the height of the cylinder using the same ruler.
- Apply the radius and height to the formula V = πrh, estimating π as 3.14 for simplicity.
- Calculate the volume by squaring the radius, multiplying by the height, and then by 3.14.
Summary:
Estimating volume with a ruler is quick and easy, making it suitable for non-critical tasks where estimates suffice. The disadvantage is that estimates can be inaccurate, potentially leading to errors in calculations where precision is pivotal.
Utilizing Water Displacement
For irregularly shaped objects or ones that can’t be easily measured with a ruler, the water displacement method can be applied. This method is based on the fact that an object submerged in water will displace its volume in water.
Detailed Steps:
- Fill a graduated cylinder or overflow can with water to a specific volume marker.
- Submerge the circular object, if it fits, or the cylinder it’s a part of, into the water.
- Observe the new water level or the volume of water that has overflowed.
- The difference in the water level before and after the object’s submersion is the volume of the object.
Summary:
Water displacement is an effective method for finding volume when direct measurement isn’t possible. It’s a principle commonly used in scientific applications. However, this method might not be suitable for objects that are water-soluble or can be damaged by water.
Using Mathematical Software
Advanced mathematical software and graphing calculators can easily calculate volumes of circles in the context of cylinders or spheres. They often have built-in functions for these calculations.
Detailed Steps:
- Input the radius and height of the cylinder into the software.
- Access the formula or function within the software designed to calculate the volume of cylinders.
- Allow the software to compute the volume based on your inputs.
- Read the calculated volume from the display or output window.
Summary:
Mathematical software vastly simplifies volume calculations and minimizes human error. It’s particularly beneficial for complex shapes. The downside could be the cost of the software and the learning curve to use it effectively.
Calipers for Precision Measurement
Calipers are precision tools that can measure the radius and height of a cylinder with high accuracy. These tools are preferable when exact measurements are required.
Detailed Steps:
- Use the caliper jaws to measure the diameter of the cylinder’s base and divide by two for the radius.
- Adjust the caliper for depth measurement and measure the height of the cylinder.
- Apply these measurements to the volume formula.
- Calculate as per the steps mentioned in the “Using Cylinder Volume Formula” section.
Summary:
Calipers provide highly accurate measurements, making them ideal for detailed work and professional applications. The disadvantage is their cost and the need for skill in usage.
Substitute π for Simplified Calculation
For quick mental calculations or situations where a perfect π value isn’t needed, you can substitute π with a more manageable number.
Detailed Steps:
- Measure the radius and height of the cylinder.
- Use 3 as a substitute for π to simplify the mental math.
- Calculate the volume with the adjusted formula V = 3 * r * h.
Summary:
This offers a very rough estimate of volume and is only beneficial for quick, non-precise assessments. Substituting π this way leads to a significant loss of accuracy.
Referencing Pre-calculated Charts
There are volume charts available for standard cylinder sizes, which can speed up the process without any calculations.
Detailed Steps:
- Measure the radius and height of the cylinder.
- Look up a chart that matches the measured dimensions.
- Find the pre-calculated volume on the chart.
Summary:
Using pre-calculated charts saves time but is limited to the sizes listed. If the cylinder’s dimensions don’t exactly match, it’s an approximation at best.
Apps and Online Calculators
There is a plethora of apps and online volume calculators that require just a few inputs to provide you with the volume.
Detailed Steps:
- Provide the radius and height of the cylinder to the app.
- The app calculates the volume for you.
Summary:
Apps and online calculators are extremely user-friendly and accessible, but they do require trust in the app’s accuracy and have a dependency on technology.
Approximation by Scaling Model Cylinders
You can use scale models to approximate the volume of larger cylinders by using a smaller, proportional model.
Detailed Steps:
- Create or obtain a smaller model of the cylinder at a known scale.
- Calculate the volume of the smaller model.
- Scale the volume up to the actual size.
Summary:
This is useful for educational purposes or visual demonstrations, but it’s not precise and won’t replace actual calculations.
Simple Geometry Sets for Classroom Use
In educational settings, simple tools like a compass and rulers can help students learn to calculate volumes by constructing and measuring paper models of cylinders.
Detailed Steps:
- Use a compass to draw a circle and cut it out for the base.
- Measure and cut a rectangle for the side, with the length equal to the circumference of the base and the height desired.
- Assemble into a cylinder and use tactile understanding to learn about volume.
Summary:
This hands-on approach is great for learning and understanding core principles of volume. However, it’s not a method for precise calculations and is best suited for demonstration purposes.
In conclusion, calculating the volume of a circle, which typically refers to the volume of a cylindrical object or space, can be done through a variety of methods suited for different needs and situations. From precise mathematical formulas to hands-on educational tools, each method offers its own advantages. The key is to choose the one that best fits the circumstance, whether that is the need for precision or a simple estimate. Regardless of the method, mastering the volume calculations of circles will undoubtedly serve as a valuable skill in many practical and academic endeavors.
FAQs:
Q1: Can a circle have a volume?
A1: No, a circle is a two-dimensional shape and does not have volume. Volume calculations typically involve the cylinder or sphere that the circle is a part of.
Q2: Why is π used in calculating the volume of a cylinder?
A2: π (pi) represents the ratio of the circumference of a circle to its diameter and is pivotal in the formula for the area of the circle’s base, which is used to calculate the volume of a cylinder.
Q3: What is the most accurate method to calculate the volume of a cylindrical object?
A3: Using precise tools like calipers to measure the dimensions followed by applying the cylinder volume formula will give the most accurate calculation of volume.
Q4: How can you calculate the volume without measuring tools?
A4: You can use the water displacement method or reference pre-calculated charts for an estimate without direct measurements.
Q5: Is it necessary to use the exact value of π in volume calculations?
A5: For precise calculations, using the accurate value of π is important. However, for estimates or simplified mental math, a rounded value or approximation of π can be used.