Understanding how to calculate the volume of a three-dimensional space, such as a rectangular prism, is a fundamental skill. It’s applicable not just in various fields of STEM (Science, Technology, Engineering, and Math), but also in everyday life situations, like figuring out how much space you have to store boxes in a room or how much water a pool can hold. Grasping this concept involves a basic mathematical formula, and once you know how to apply it, finding the volume of a rectangular prism is straightforward.
The Basic Formula Approach
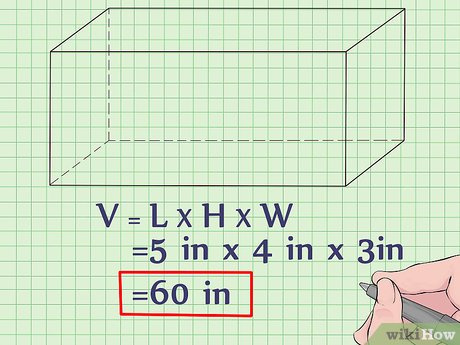
When it comes to finding the volume of a rectangular prism, the most straightforward method is using the basic formula. This principle is founded on the idea that volume is the product of an object’s length, width, and height.
Steps:
- Identify the length (L), width (W), and height (H) of the rectangular prism. These are typically the longest side, the shorter side, and the vertical side, respectively.
- Make sure all measurements are in the same unit. If they’re not, convert them into the same units (for example, all in centimeters or inches).
- Execute the formula: Volume (V) = Length (L) x Width (W) x Height (H).
- Multiply the length by the width and then by the height.
- Record your answer which is the volume of the rectangular prism in cubic units.
Summary:
The basic formula method is easy to understand and effective for calculating volume. However, its simplicity is also a limitation as it cannot be applied to more complex shapes without modification.
Using Measurement Tools
Sometimes, the dimensions of a rectangular prism are not provided, and you need to measure them yourself.
Steps:
- Select appropriate tools for measurement, such as a ruler or a tape measure.
- Carefully measure the length, width, and height of the rectangular prism.
- Record the measurements, ensuring they are all in the same unit.
- Apply the volume formula: Volume = Length x Width x Height.
- Compute the volume using your recorded measurements.
Summary:
This method is practical and hands-on, encouraging a deeper understanding of the dimensions of objects. However, accuracy is dependent on the precision of your measuring and may introduce a margin of error.
Volume by Water Displacement
This hands-on method uses the principle of water displacement to measure volume, which is ideal for irregularly shaped prisms or when precise measurements are hard to obtain.
Steps:
- Fill a graduated cylinder or overflow can with water, noting the initial level of water.
- Submerge the rectangular prism in the water completely.
- Determine the new water level after the prism is submerged.
- Calculate the change in water level, which corresponds to the volume of the prism.
Summary:
This method is excellent for visual and tactile learners and for items that can be submerged without damage. The downside is that it’s limited to waterproof items and can be less accurate due to water spillage or evaporation.
Exploiting Symmetry
For prisms that are symmetric, you can simplify the measuring process and ensure accuracy by focusing on the repeated measurements of the symmetrical sides.
Steps:
- Identify the sides that are symmetrical.
- Measure one of the symmetrical sides to get the length, width, and height.
- Verify by measuring the parallel sides to ensure they are identical.
- Use the volume formula with these dimensions.
Summary:
This method promotes efficiency and may increase measurement accuracy. However, if the symmetry is assumed and not verified, it may result in incorrect volume calculations.
Using Unit Cubes
This tactile method involves simulated or actual unit cubes to teach how volume is a measure of how many of these cubes can fit within a prism.
Steps:
- Understand what a unit cube is (a cube where each side is one unit in length).
- Determine how many unit cubes fit along the length, width, and height of the rectangular prism.
- Multiply these three numbers together to find the volume.
Summary:
Unit cubes provide a clear, concrete representation of volume, making it ideal for beginners. Its downside is practicality, as using physical cubes is not always feasible, especially for large or theoretical prisms.
Comparative Analysis
In this method, you compare the rectangular prism’s volume to a known volume, thus finding the relative size.
Steps:
- Find a reference object with a known volume.
- Estimate how many times this reference fits into your rectangular prism.
- Multiply the known volume by your estimation to determine the volume of the prism.
Summary:
Comparative analysis is intuitive and can be done without formulas; however, it requires a good spatial understanding and results in rough estimates rather than precise measurements.
Algebraic Expressions
Algebra can help find the volume if one of the dimensions in terms of the others if it’s not directly measurable.
Steps:
- Set up an equation using the formula where one dimension is unknown (e.g., V = x * W * H).
- Substitute the known volume and one other known dimension into the equation.
- Solve the algebraic equation for the unknown dimension.
- Now find the volume using all known dimensions.
Summary:
Algebraic expressions are powerful for solving problems with missing information. On the flip side, this process requires a basic understanding of algebra, which might not be accessible to everyone.
Graphical Representation
Drawing a diagram can help visualize the problem when learning how to calculate volume—it translates abstract numbers into a visual format.
Steps:
- Draw a to-scale model of the prism on graph paper.
- Label the dimensions on your drawing based on the measured or given values.
- Use the formula on the diagram to understand how volume is calculated.
- Calculate the actual volume.
Summary:
Graphical representation can make understanding volume more intuitive. However, this method may be less useful for those who are not visually inclined.
Computer-Aided Design (CAD) Software
CAD software is used to model the rectangular prism and calculate its volume digitally, which is useful in design and engineering.
Steps:
- Input the dimensions of the prism into the software to create a 3D model.
- Use the software’s volume calculation tool to find the volume.
- Verify the volume by checking the input dimensions and computation.
Summary:
This high-tech method is precise and streamlines the volume calculation process. Its downside is that it requires access to and knowledge of specialized software.
Mobile Apps
Several mobile applications can calculate the volume of a rectangular prism by inputting the dimensions or even by using augmented reality.
Steps:
- Download a volume calculator or 3D scanner app.
- Enter the dimensions into the app or scan the prism if the app supports augmented reality.
- The app will compute and display the volume.
Summary:
Using mobile apps can be very convenient and user-friendly, with the downside of relying on the accuracy of digitized measurements or inputs.
In conclusion, calculating the volume of a rectangular prism can be approached from various angles, whether you’re using a simple formula or leveraging technology. The key is to understand the principles of length, width, and height and their interplay in defining volume—which you can then apply with the method that suits your context best.
FAQs:
Q1: Can I calculate the volume of a rectangular prism if I only know two dimensions?
A1: If you only have two dimensions, you cannot calculate the volume without additional information. Volume requires three dimensions—length, width, and height.
Q2: Does the order of multiplication matter when calculating volume?
A2: No, the order in which you multiply the dimensions does not matter. Due to the commutative property of multiplication, you will get the same result regardless of order.
Q3: How do I convert units when calculating volume?
A3: To convert units, you multiply (or divide) your measurements by the conversion factor between the units. For example, to convert from centimeters to meters, you divide each dimension by 100 before calculating the volume.







